Święty Anzelm przedstawił następujące rozumowanie (nazwane argumentem ontologicznym), obalające tezę, że Bóg nie istnieje:¹

1. Nawet głupiec rozumie pojęcie „Bóg” gdy twierdzi, że „Bóg nie istnieje”.
2. Pod pojęciem tym rozumiemy coś najdoskonalszego, czyli coś takiego, że nie możemy nawet pomyśleć o czymś doskonalszym.
3. Jednak coś co istnieje naprawdę jest doskonalsze niż coś co istnieje tylko w umyśle.
4. Jeśli głupiec twierdzi, że Boga nie ma, to uważa że jedynie rozumie (ma w umyśle) pojęcie, które do niczego się nie odnosi.
5. Ale przecież może sobie wyobrazić, że tej doskonałości w jego umyśle odpowiada coś istniejącego naprawdę. Czyli może sobie wyobrazić coś doskonalszego. To przeczy tezie, że najdoskonalsze jest/było pojęcie Boga nie istniejącego. Musi zatem Bóg istnieć realne – bo tylko odnoszące się do niego pojęcie może być pojęciem doskonałości.

Historia tego argumentu jest bardzo ciekawa, bo pokazuje zmiany w relacji między nauką i religią.

Religia przestała być podstawowym sposobem objaśniania świata. Dlatego takie argumenty należą obecnie do sfery kultury i nie są oparte na dedukcji. Pozbawiony pretensji do ścisłości argument ontologiczny może wyglądać następująco:

1. Samo istnienie idei Boga stanowi wystarczającą podstawę do tego, by rozważać Jego istnienie. Ta myśl św Anzelma została podjęta przez Jana Pawła II w encyklice "Fides at Ratio". Papież pisze tam²: "Już sama zdolność poszukiwania prawdy i stawiania pytań podsuwa pierwszą odpowiedź. Człowiek nie podejmowałby poszukiwania czegoś, o czym nic by nie wiedział i co uważałby za absolutnie nieosiągalne."

2. Akceptując pojęcie Boga jako bytu najdoskonalszego, musimy uznać iż byt ten istnieje realnie. Skoro bowiem Bóg jest bytem najdoskonalszym, to „w taki sposób realnie istnieje, że nawet nie można pomyśleć, iż nie istnieje” [Mieczysław Gogacz³].

W zupełnie odwrotnym kierunku rozwija się światopogląd naukowy, którego wielu wyznawcom marzy się „dyktatura racjonalności”. Kultura i religia może według nich odpowiadać na pewne potrzeby ludzi, ale na pewno nie jest to dobry sposób na dotarcie do fundamentalnych prawd o świecie w którym żyjemy.

Podstawowym wnioskiem z opisanej poniżej historii jest jednak to, że ścisłe oraz pewne odpowiedzi mogą być udzielone wyłącznie wtedy, gdy postawimy właściwe pytania. Pytania te pozostają różne dla religii i nauki. Argument ontologiczny pojawia się w punkcie ich styczności.

Krytyka Kanta

Z argumentacją św. Anzelma nie zgadzał się Immanuel Kant. Według niego możemy porównywać tylko cechy obiektów, a istnienie nie jest cechą. Możemy zatem stwierdzić, że coś jest mniej lub bardziej czerwone, że coś ma rozum lub nie. Nie można jednak stwierdzić, że coś ma lub nie ma cechy istnienia. 

Dowody w logice modalnej

Immanuel Kant wielkim filozofem był, więc na pewno miał rację ;-). Później pojawiły się jednak logiki modalne, które pozwoliły na formalny dowód tezy Anzelma. Poniżej jeden z takich dowodów (oznaczenia pochodzą od Andrzeja Biłata⁴). 

Założenia:

• AA: Byt doskonały to taki, że jeśli on istnieje, to istnieje z konieczności :

  p0 → L(p0)

  (Czyli byt doskonały z definicji jeśli istnieje, to od razu w każdym świecie możliwym)

• AL: Jest możliwe, że byt doskonały istnieje: M(p0).

Skrót AA pochodzi od określania „zasada Anzelma”, natomiast AL od „zasada Leibniza”⁵.

Oznaczenia:

• p0 reprezentuje zdanie „Byt doskonały istnieje”,
• L to operator modalny konieczności (jest konieczne),
• M to operator modalny możliwości (jest możliwe),

Dowód⁶:

1. M(p0) : AL

2. M(L(p0)) : AA zastosowane do (1) z uwzględnieniem reguły opisanej poniżej

3. M(L(p0)) → p0 : Twierdzenie logiki modalnej (zobacz Tw1⁷)

4. p0 : reguła odrywania⁸ zastosowana do (3) z uwagi na (2)

W kroku (2) zastosowano intuicyjnie zrozumiałą regułę (jeśli w jakimś możliwym świecie występują przesłanki, to i akceptujemy wniosek)⁹:

X→Y
------------
M(X) → M(Y)

No to mamy solidny dowód? Chyba niekoniecznie. Dowód ten jest oparty na założeniach, które nie są wcale oczywiste. Mogą być podważane na przykład tak jak czyni to Jan Woleński w tekście „Gaunilon dzisiaj”¹⁰: [Lepiej byłoby] powiedzieć, że dowód Lematu Leibniza¹¹[zgodnie z którym istnienie bytu najdoskonalszego nie jest niemożliwe] i dalsze kroki [argumentu ontologicznego] odbywają się w ramach pewnej teorii formalnej dotyczącej pojęć modalnych, a nie mają charakter czysto logiczny¹².

Woleński wielkim masonem jest – więc na pewno ma rację ;-).

Nowe sformułowanie problemu

Po co logicy chcą się wikłać w problemy istnienia i tworzą przy tym jakieś mało intuicyjne konstrukcje? Jest to niezrozumiałe zwłaszcza w ojczyźnie Tarskiego, który sformułował definicję prawdy bez konieczności rozważania istnienia bytów. 

Czy można przeprowadzić dowód bez wikłania się w takie problemy? Tak - i to na dwa sposoby:

1. Posługując się algebrą i teorią mnogości możemy sformułować teorię, która obejmuje byt najdoskonalszy. Jeśli ktoś zaakceptuje taką teorię jako adekwatną do opisu rzeczywistości – musi przyjąć płynące z niej wnioski.

2. Możemy też analizować prawdziwość i sensowność wypowiedzi o bycie najdoskonalszym. Czyli rozważamy to zagadnienie na gruncie semantyki języka¹³. Formalizacja zagadnienia prowadzi do abstrahowania od znaczenia wypowiedzi języka w odniesieniu do realnie istniejących bytów.

Czyli właściwe dla racjonalnej analizy pytanie nie brzmi: czy Bóg istnieje?

Możemy jedynie pytać:

Czy istnieją teorie racjonalnie opisujące świat, a obejmujące dowód istnienia bytu doskonałego?

Czy i kiedy wypowiedzi o istnieniu / nieistnieniu bytu doskonałego są zrozumiałe? Czy i w jakich warunkach można dowieść ich prawdziwości? 

Analiza algebraiczna

Pojęcie światów możliwych jest intuicyjnie proste. Jednak traktując je jako struktury algebraiczne możemy się nim posługiwać bez tych okropnych formalizmów logiki modalnej. Gdy posługujemy się czystą algebrą, nie ma miejsca na żadne niejasności. Jeśli zaakceptujemy przyjęty model (założenia), to musimy zaakceptować uzyskany rezultat. Problem jedynie w tym, że różnych algebraicznych modeli rzeczywistości może być wiele (w trakcie pisania tego artykułu powstało co najmniej trzy). 

Zdefiniujmy strukturę:

Uniwersum = (Światy, Byty, Pojęcia, Istnienia, Rozumienie, Doskonałość, Bóg)

Zbiory:

• Światy: światy możliwe,

• Byty: obiekty istniejące w którymś ze światów,

• Pojęcia: zbiór określeń używanych do opisu świata (odniesień do bytów),

Relacje:

• Istnienia: Światy x Byty = obiekty istniejące w danym świecie możliwym,

• Rozumienie: Świat x Pojęcia x Byty = powiązanie pojęć z bytami na które one wskazują; jest to funkcja przyporządkowująca pojęciom w danym świecie możliwym byty; czyli jeśli trójka (s,p,b) należy do relacji Rozumienie, to oznacza iż w świecie s pojęcie p odnosi się do bytu b;

• Doskonałość: Światy x Pojęcia x Pojęcia = relacja doskonałości, oznaczana znakiem >; wyznacza ona porządek bytów w obrębie świata. Porządek ten spełnia dodatkowe warunki opisane poniżej.

Komentarz: w tym modelu Byty są wspólne dla wszystkich światów możliwych (zakładamy, są stałe - tak jak idee Platona). Relację doskonałości zdefiniowano w obrębie pojęć (a nie bytów), bo jest to jest bliższe intuicyjnemu rozumieniu naukowej metody badania rzeczywistości. 

Definicja Boga (DB):

Bóg (B) jest bytem najdoskonalszym. Czyli dla każdego jego rozumienia [(s,pB,B) należy do Rozumienie], dla każdego p różnego od pB mamy pB > p w świecie s.

Warunki doskonałości:

• Warunek istnienia (D1): zbiór Byty nie jest pusty, a w każdym świecie istnieje co najmniej jedno pojęcie odnoszące się do jakiegoś bytu istniejącego - czyli dla każdego s istnieje b takie, że (s,b) należy do Istnienia oraz (s,p,b) należy do Rozumienie.

• Warunek wyższości bytu istniejącego  (D2): Byt istniejący jest doskonalszy od nie istniejącego. Jeśli w świecie s dla mamy (s,B) należy do Istnienie, oraz (s,pB,B) należy do Rozumienie, to dla każdego p takiego że (s,p,X) należy do Rozumienie, a (s,X) NIE należy do Istnienie mamy pB>p. Czyli byt rozumiany przez najdoskonalsze pojęcie w świecie s, musi istnieć.

• Możliwość istnienia bytu najdoskonalszego (D3): dla co najmniej jednego świata s zachodzi (s, pB, B).

Teza Anzelma:

Bóg istnieje – czyli byt B spełniający definicję DB istnieje w każdym możliwym świecie [(s,B) należy do Istnienia].

Dowód:

1. W każdym świecie musi istnieć byt najdoskonalszy:

1. załóżmy, że w jakimś świecie s nie istnieje takie b, że (s,pb,b) należy do Rozumienie i (s,b) należy do Istnienia oraz pb>p dla każdego p;

2. z uwagi na warunek istnienia (D1) musimy przyjąć istnienie B’, czyli (s,B’) należy do Istnienia oraz (s,pB’,B’) należy do Rozumienie;

3. na mocy relacji doskonałości (D2), pB’ > pb w świecie s, więc albo to pB’ jest tożsamy z pb albo popadamy w sprzeczność z założeniem 1a).

2. Byt doskonały (spełniający definicję DB) musi istnieć w każdym świecie s:

1. z możliwości istnienia (D3) wynika, że w pewnym świecie s0 zachodzi (s0, pB, B).

2. gdyby w jakimś świecie s nie zachodziło (s, pB’, B), to z uwagi na warunek istnienia (D1) musi istnieć inny byt E, czyli (s,E) należy do Istnienia a (s,pE,E) do Rozumienie.

3. Jednak na mocy warunku konieczności mielibyśmy wówczas w świecie s pE>pB – co jest sprzeczne z definicją (DB).

Mamy więc istniejący byt doskonały (1), który musi istnieć w każdym możliwym świecie (2) c.b.d.o.

Pozostaje pytanie czy taki model opisuje naszą rzeczywistość (zgadza się z naszym oglądem świata). W zasadzie sprowadza się to do pytania o warunki doskonałości (w szczególności D2 i D3).

1. Czy należy dopuścić możliwość istnienia bytu najdoskonalszego (D3)? To pytanie o istnienie realne granicy dla pewnego porządku. W tym wypadku dotyczy doskonałości, ale kwestia jest bardziej uniwersalna. Jeśli na przykład weźmiemy liczby naturalne, to możemy zdefiniować nieskończoność jako granicę do której zmierza uporządkowany relacją większości ciąg liczb. Pojawia się pytanie: czy taka granica istnieje tak jak liczby, czy też to tylko inne sformułowanie informacji o tym, że nie istnieje największa liczba? Można to wyjaśnić przez analogię. Na pytanie dokąd idziesz możemy usłyszeć odpowiedź: „do sklepu”, albo „donikąd”. Czy donikąd istnieje, czy też należy rozumieć to jako: „nie wiem” lub „nie chcę ci powiedzieć”?

2. Założenie D2 sprowadza się do przekonania, że prawda o świecie jest lepsza od ułudy (opowieści o nie istniejących bytach). Założenie to można zastąpić przez Warunek konieczności (D2'): byt doskonały musi być z konieczności bytem istniejącym, czyli musi istnieć i być opisany przez pewne pojęcie w każdym świecie możliwym [jeśli w świecie s1 dla każdego p1 zachodzi pB1>p1 oraz (s1,pB1,B) należy do Rozumienie, to w każdym świecie s2 mamy:(s2,pB2,B) należy do Rozumienie i (s2,B) należy do Istnienie].  Czy w każdym możliwym świecie możemy zakładać zrozumienie pojęcia doskonałości? Tu możemy się odwołać do doświadczenia, które mówi nam, że pojęcie doskonałego Boga jest znane w każdej kulturze.  

Możemy zatem sformułować taką teorię w której nieskończoność (u Anzelma doskonałość) może istnieć (tak jak liczba). Argument Anzelma sprowadza się do tego, że jeśli odrzucimy tego rodzaju istnienie, to opisany model świata staje się absurdalny. Tak jest rzeczywiście, jeśli odrzucimy tylko część warunków. Na przykład odrzucając D3 pozostawimy D2. Dlatego możemy jedynie odrzucić lub przyjąć taki model w całości. 

Analiza semantyczna

Przedstawiony powyżej model algebraiczny może służyć do zdefiniowania semantyki języka. Wystarczy dodać wyrażenia języka i relacje między tymi wyrażeniami i pojęciami

Wstęp do formalizacji

Zakładamy zatem, że wypowiedzi języka odnoszą się do pojęć: pewne elementy wypowiedzi są charakterystykami lub nazwami obiektów (bytów). Odpowiadają im konkretne pojęcia. Na przykład gdy określimy sąsiada jako: 'Jan Kowalski mieszkający za ścianą', to mamy w umyśle pojęcie Jana Kowalskiego, które kojarzymy z konkretną osobą (bytem): Janem Kowalskim. Wyjaśnia to poniższy rysunek (choć odwołuje się on do naszych intuicji – możemy traktować zdefiniowane klasy obiektów czysto formalnie).

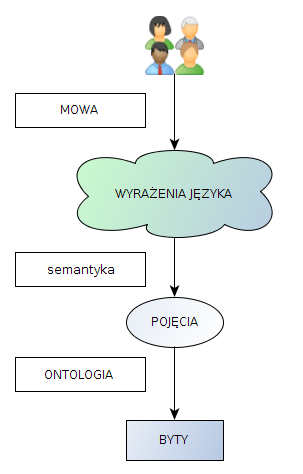
W oparciu o pojęcia definiuje się znaczenia (semantykę) wyrażeń (do czego odnoszą się określenia lub nazwy własne). Pojęcia mogą być związane z konkretnymi bytami, ale ich istnienie rozważamy jedynie w odniesieniu do pojęć, a nie do wyrażeń języka których używamy mówiąc o bytach. Byty można porównywać według różnych kryteriów, tworząc relacje między nimi – w tym relacje pozwalające ocenić ich doskonałość. Jeśli pojęcia którymi operujemy mają być adekwatne, wspomniane relacje muszą się na nie przenosić.

Przyjmując taką semantykę języka można przeprowadzić logiczną analizę argumentu Anzelma. Musimy jednak przyjąć w tym celu warunki wstępne:

1. Przy logicznej analizie nie odnosimy się wprost do rzeczywistości, tylko wyrażeń języka oraz pojęć.

2. Dla tych spośród wyrażeń języka, które są sensowne (zrozumiałe), można nie tylko podać ich znaczenie, ale też oznaczanie¹⁴: wskazywać na pojęcia do których się one odnoszą (do jednego pojęcia może odnosić się wiele wyrażeń języka). Czyli przyjmujemy semantykę referencyjną.

Teza Anzelma

1. Akceptując tezę „możliwe, że Bóg rozumiany jako byt doskonały istnieje” zgadzamy się na:

a. Pojęcie bytu najdoskonalszego. Czyli akceptujemy porządek doskonałości: pojęcie bytu najdoskonalszego przewyższa w porządku doskonałości wszelkie inne pojęcia.

b. Sensowność odniesień do Boga – czyli wyrażenie „Bóg” jest zrozumiałe (odnosi się do znanych nam pojęć).

c. Definicję Boga jako bytu doskonałego, czyli doskonalszego od każdego innego bytu.

2. Mówiąc o Bogu istniejącym, wyrażamy przekonanie o prawdziwości wypowiedzi oznajmiających jego istnienie.

Argument Anzelma wychodząc od wypowiedzi: „możliwe, że byt najdoskonalszy istnieje” zmierza do tezy: „nie można zaprzeczyć istnieniu bytu najdoskonalszego”.

To jest najważniejszy moment analizy. Nie musimy dociekać realnego istnienia bytów. Wystarczy, gdy przyjmiemy, że ktoś mógł powiedzieć prawdę na temat ich istnienia (na przykład wierzymy w prawdziwość słów Ewangelii Chrystusa). Od tej chwili możemy poprzestać na rozważaniu kwestii sensowności i prawdziwości wypowiedzi.

3. Jednym z istotnych elementów Argumentu Anzelma jest przyjęcie, że doskonałość jest związana z istnieniem. Czyli jeśli uznamy, że prawdziwe są wypowiedzi o istnieniu jakiegoś bytu, to uznajemy równocześnie, że jest on doskonalszy od tych bytów, o istnieniu których nie możemy orzec prawdy. Przykładowo mamy:

• prawdziwe jest zdanie „Chrystus umarł na krzyżu”

• nie jest prawdziwym zdanie „Zeus jest postacią prawdziwą”

uznając te tezy możemy wysnuć wniosek, że pojęcie  „Chrystus” jest doskonalsze od pojęcia „Zeus”. 

Argumentacja

Oznaczenia:

• L - język zawierający wyrażenia;
• D – dziedzina, czyli zbiór pojęć do których odnoszą się wyrażenia w z języka L;
• T – teza teistyczna, czyli wyrażenie w odnoszące się do Boga (na przykład: „Bóg istnieje” lub „Bóg jest stworzycielem świata”);
• M(L) – metajęzyk dla języka L
• DM – dziedzina w której określono semantykę metajęzyka

Objaśnienia:

1. Mówimy, że wyrażenie w języka L jest spełnione (w rozumieniu Tarskiego) w danej dziedzinie D, jeśli przy pewnym wartościowaniu (odniesieniu zmiennych/zaimków do pojęć) wyrażenie to jest prawdziwe. Na przykład wyrażenie „x > 2*x” jest spełnione w dziedzinie liczb rzeczywistych (jeśli x jest dodatnie - wyrażenie jest prawdziwe).

2. W metajęzyku M(L) możemy formułować tezy dotyczące wyrażeń języka L. W szczególności możemy dla każdego wyrażenia w z języka L sformułować tezę w’: „w” jest spełnione(*) w dziedzinie D. Gwiazdkę dodano, aby zwrócić uwagę, że oczywiście nie przy każdym wartościowaniu wyrażenie jest spełnione. Językowi M odpowiada dziedzina DM do której odnoszą się wyrażenia z M (czyli DM musi zawierać D).

Założenia:

1. Dziedzina D zawiera pojęcia do których odnoszą się wyrażenia języka L. W tym (konsekwencje akceptacji zdania „możliwe, że Bóg jako byt najdoskonalszy istnieje”):

   1. pojęcie bytu najdoskonalszego: pB takie, że dla każdego p zachodzi pB>p;

   2. pojęcie Boga jako bytu najdoskonalszego;

   3. pojęcie Boga jako bytu istniejącego.

2. Pojęcie bytu istniejącego jest doskonalsze od pojęcia bytu nie istniejącego.

Teza:

Nie można sensownie zaprzeczyć istnieniu Boga jako bytu najdoskonalszego.

Czyli jeśli mamy zdanie (T) języka L: „Bóg jako byt najdoskonalszy istnieje”

to nie można zaprzeczyć zdaniu M(L):   "Zdanie (T) jest sensowne i prawdziwe".

Dowód:

1. Z założenia 1 wynika, że możemy w języku L sformułować tezę o istnieniu Boga (T) – wystarczy skreślić „możliwe, że”.

2. Jeśli teza (T) o istnieniu Boga nie odnosi się do żadnego sensownego pojęcia – dotyczy to także zaprzeczenia tezy (T), co kończy dowód.

3. Załóżmy zatem, że  teza (T) odnosi się do pojęcia pB (a więc jest zrozumiała). Wówczas z założenia 1 wynika iż pB > p dla każdego p różnego od pB, należącego do dziedziny D.

4. Jeśli pB nie byłoby tożsame z pojęciem Boga istniejącego (pE), to byłoby pE>pB – co stoi w sprzeczności z 3. Jeśli zatem pB to pojęcie Boga istniejącego - teza (T) musi być prawdziwa.

5. Teza „nieprawda, że (T) to jest sensowne i prawdziwe” musiałaby być spełniane w DM obejmującej D. A więc albo teza (T) musiałaby być nieprawdziwa – co jest sprzeczne z 4), albo (T) musiałoby być niezrozumiałe – co jest sprzeczne z 3). c.b.d.o.

Komentarz

Jak się okazuje akceptacja tezy „możliwe, że Bóg jako byt najdoskonalszy istnieje” w zasadzie przesądza o tym, że nie da się sensownie zaprzeczyć istnieniu Boga. Wypowiedzi dotyczące Boga mogą być zrozumiałe nawet dla ateisty odrzucającego teistyczne hipotezy o istnieniu Boga. Jednak semantyka takich wypowiedzi nie może być definiowana w oparciu o tożsamość znaczenia i oznaczania (semantyka referencyjna)15 oraz pojęcia jakimi operuje człowiek religijny. Inaczej nie wiadomo do czego odnosi się teza „Boga nie ma”. Czyli takie „wyznanie wiary”  należy do sfery kultury i nie podlega logicznej analizie.

Podsumowanie

Pozbywając się spekulacji i logiki modalnej, stajemy na twardym gruncie logiki klasycznej, semantyki logicznej i algebry. Możemy badać struktury języka (zob. analiza semantyczna) lub tworzyć formalne teorie, używając algebry i teorii mnogości. Dzięki temu udaje się osiągnąć nietrywialne rezultaty nawet w dziedzinach, które wydawały się być predysponowane do nie kończących się sporów. W miejsce sporu o prawdziwość opisu świata pojawia się analiza warunków prawdziwości i sensowności wypowiedzi. Natomiast w miejsce sporów ontologicznych - badamy zbiory i struktury (w tym światy możliwe).

Dziękuję Maciejowi Wawro za krytyczne uwagi do kolejnych wersji tekstu, które przyczyniły się do (mam nadzieję) jego znacznego ulepszenia.

Przpisy: