Maszyna Turinga jako powszechnie przyjęty model obliczeniowy ma kilka wad. Najważniejszą z nich jest koncentracja na złożoności czasowej problemów (złożoność pamięciowa jest zawsze mniejsza od czasowej, więc nie ma potrzeby jej brać pod uwagę). W praktyce musimy uwzględnić zarówno czas jak i zasoby pamięci potrzebne do rozwiązania problemu. Jeśli w pamięci komputera zawarte są częściowe rozwiązania, może to przyspieszyć obliczenia. Można też poddać niezależnej analizie złożoność pamięciową – optymalizując ją na przykład przez kompresję.
Niniejszy artykuł pokazuje perspektywy badań nad złożonością, jakie otwierają się dzięki uwzględnieniu innego modelu obliczeniowego: systemów iteracyjnych.
Jedna z proponowanych koncepcji złożoności (sieci logiczne) jest obecnie rozwijana1, co potwierdza słuszność wniosków wysnutych na podstawie poniższej analizy.
System iteracyjny jako model obliczeniowy
Maszyna Turinga nie jest jedynym znanym modelem obliczeniowym. Wcześniej sformułowano rachunek lambda, a później systemy iteracyjne (Z. Pawlak)2. Powstał też model bardziej zbliżony do współczesnych komputerów: maszyny RAM3. Model maszyny Turinga z nieskończoną taśmą nie jest ani intuicyjny, ani praktyczny. Dlatego w niniejszym artykule analizę złożoności opartą o system iteracyjny.
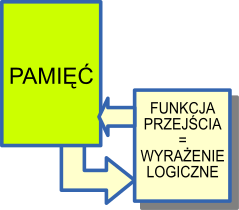
Składa się on z pamięci, funkcji przejścia i zegara w takt którego wynik funkcji przejścia zapisywany jest do pamięci. Jeśli przyjmiemy, że pamięć składa się z elementów jednobitowych (0 lub 1), to funkcja przejścia staje się zbiorem funkcji logicznych, z których każda na podstawie zawartości pamięci wylicza nową wartość jednej komórki pamięci.
Model zaproponowany przez Z. Pawlaka nie obejmuje wydzielonego wejścia i wyjścia. Jednak nic nie stoi na przeszkodzie, aby dokonać stosownego rozszerzenia. W pamięci możemy więc teoretycznie wydzielić wejście oraz wyjście.
Wejście to część pamięci (teoretycznie może być cała) która zawiera dane wejściowe dla programu zaimplementowanego w postaci systemu iteracyjnego. Wyjście to z kolei część pamięci, której zmiana jest celem programu. Zmiana tej części pamięci oznacza zakończenie programu.
Obliczenia polegają na powtarzaniu zapisywania nowego stanu w pamięci tak długo, aż zostanie osiągnięty określony stan końcowy - na przykład zapisanie w części pamięci (na wyjściu) wyniku.
System iteracyjny (z określoną funkcją przejścia i zawartością początkową pamięci) oblicza wynik dla algorytmu zdeterminowanego przez funkcję przejścia i zapisane w pamięci dane (wejście). Aby uwzględnić możliwość użycia tego modelu dla takich samych obliczeń o różnych wejściach, proponujemy używać określenia „system iteracyjny Pawlaka” dla oznaczenia konstrukcji opisanej powyżej. Klasa systemów iteracyjnych Pawlaka różniących się między sobą zawartością wejścia odpowiada programowi obliczającemu wynik algorytmu dla dowolnych danych wejściowych. W dalszej części tekstu będziemy używać konsekwentnie nazwy „system iteracyjny” dla określenia takiej właśnie klasy systemów iteracyjnych Pawlaka.
Problem możemy zdefiniować jako zbiór algorytmów (systemów iteracyjnych) takich, że dla identycznych danych wejściowych dają identyczne wyniki.
Trzy proste elementy (pamięć, funkcja przejścia i zegar) przekładają się wprost na trzy miary złożoności systemu iteracyjnego:
- wykorzystywana pojemność pamięci;
- złożoność funkcji przejścia;
- czas
Złożoność pamięciowa może być mierzona ilością wykorzystywanych jednobitowych elementów pamięci.
Złożoność funkcji przejścia to suma ilości operatorów logicznych (bramek) wykorzystywanych w zdefiniowaniu wszystkich funkcji logicznych składających się na funkcję przejścia.
Natomiast złożoność czasowa to maksymalna ilość cykli zegara w czasie obliczeń.
Jeśli rozważamy konkretny system iteracyjny (program dla określonego algorytmu), to możemy założyć, że złożoność pamięciowa i złożoność sieci logicznej są stałe (maksymalna ilość wykorzystywana przy różnych danych), natomiast czas może się różnić zależnie od wielkości danych. To założenie nie jest teoretycznie konieczne, ale sprawia że model staje się intuicyjnie prosty.
Dla każdego problemu możemy stworzyć programy z minimalną pamięcią lub minimalną złożonością funkcji przejścia (a także szereg pośrednich):
- Zapisane w pamięci wszystkie możliwe wyniki obliczeń – wtedy obliczenia polegają na prostym odczycie ich na podstawie danych wejściowych. Funkcja przejścia jest pomijalna (obliczenia wykonane w jednym kroku)4.
- Złożona funkcja przejścia wylicza od razu wynik na podstawie danych wejściowych (początkowo w pamięci nie ma niczego poza danymi wejściowymi).
Zarys dowodu:
1. Możliwość zapisu wyników w pamięci jest trywialna.
2. Weźmy dowolny algorytm ze zdefiniowaną funkcją przejścia i pewną zawartością pamięci (wejścia). Jeśli algorytm wykonuje obliczenia w n krokach, możemy te obliczenia zapisać w postaci ciągu tych funkcji wchodzących w skład funkcji przejścia, które w kolejnym kroku wyliczyły nową zawartość pamięci. Ta wyliczona wartość jest wejściem dla funkcji użytych w następnym kroku. Nie musimy więc jej zapamiętywać, jeśli połączymy odpowiednio wyjście z funkcji użytych w poprzednim kroku z wejściem funkcji użytych w kroku następnym. W ten sposób skraca się czas – aż do pojedynczego kroku. Czyli funkcja przejścia może zastąpić pamięć.
Dwie nowe miary złożoności
Podane powyżej miary złożoności są bardzo praktyczne. Możemy dla każdego systemu obliczeniowego stosunkowo łatwo oszacować potrzebną pamięć, złożoność funkcji (ilość tranzystorów w procesorze?) oraz czas obliczeń.
Gdy rozważamy złożoność problemów, bardziej interesuje nas to jak ta złożoność zmienia się dla różnych algorytmów (programów) i różnych ilości danych. Możemy przyjąć, że złożoność problemu jest wielomianowa, jeśli istnieje taki program rozwiązujący (obliczający) ten problem, że wraz ze wzrostem ilości danych żadna z wielkości: pamięć, czas i złożoność funkcji przejścia nie rośnie szybciej niż wielomianowo.
1. Złożoność funkcji logicznej
Najprostszym automatem dokonującym obliczenia jest urządzenie wejściowe połączone z urządzeniem wyjściowym, przy użyciu sieci (funkcji) logicznej. Złożoność takiej sieci można określić podając ilość stanów pamięci potrzebnych do zapamiętania parametrów i wyniku, oraz ilość elementów w sieci.
Jak pokazano w poprzednim rozdziale, możliwa jest zamiana każdego systemu iteracyjnego na maszynę z pamięcią obejmującą jedynie elementy wejścia. System iteracyjny jest w tym przypadku tożsamy z samą siecią logiczną - obliczaną w jednym kroku, bez dodatkowej pamięci. W tej sytuacji złożoność algorytmu zostaje przeniesiona w całości na funkcję przejścia.
Miarą złożoności może być ilość bramek logicznych z których tą funkcję skonstruowano.
Można także podjąć badania takiej złożoności z wykorzystaniem automatycznych metod optymalizacji funkcji logicznych, takich jak metoda tablic Karnaugh, czy metoda Quine'a-McCluskeya5.
2.Złożoność jako wielkość pamięci.
Zdefiniowanie miary złożoności w postaci wielkości pamięci nie jest tak oczywiste jak w przypadku funkcji logicznych. Jeśli zapiszemy wszystkie wyniki w pamięci to czy jeszcze można mówić o obliczeniach? Jednak analiza wpływu wykorzystania pamięci na szybkość algorytmów może być obiecującym obszarem badań. Warto też w tym miejscu zauważyć, że takie szersze spojrzenie na problem złożoności (nie tylko sieci ale i pamięć) staje się bardzo naturalne przy wykorzystaniu modelu obliczeniowego w postaci systemów iteracyjnych.
Złożoność w zadaniach trudnych
Jak wiadomo problemy NP to takie, w których znając rozwiązanie, możemy sprawdzić jego poprawność w czasie wielomianowym. Doskonale to pasuje do proponowanych w artykule miar złożoności (złożoność sieci logicznej i wielkości pamięci). Załóżmy, że zamiast zgadywać – mamy możliwość odczytania zbioru potencjalnych rozwiązań z pamięci i sprawdzenia które z nich jest poprawne w czasie wielomianowym. Problem problemów NP-zupełnych sprowadza się do tego, czy pamięć lub złożoność sieci w takim systemie muszą rosnąć wykładniczo.
Załóżmy, że mamy funkcję wyliczającą zbiór danych wynikowych dla zadanych zmiennych:
P(dane) = wynik
i możemy ja przedstawić jako złożenie dwóch funkcji:
P(dane) = F(U(dane)) = wynik
Czyli najpierw wyliczamy przy pomocy U możliwe wyniki, a potem filtrujemy wielomianowym algorytmem F wyniki poprawne dla P.
W pamięci komputera możemy zapamiętać wszystkie możliwe wyniki U(dane) dla określonego zakresu danych. Jeśli algorytm wyliczenia w oparciu o te dane będzie działał wielomianowo – to mamy komputer rozwiązujący wielomianowo problem dla pewnego zakresu danych.
Można stąd wysnuć wniosek, że zużycie pamięci jako miary wiąże się z ograniczeniem maksymalnego rozmiaru problemu (pamięć nie może rosnąć w nieskończoność).
Przypisy
1 Sanjeev Arora and Boaz Barak, Computational Complexity: A Modern Approach Princeton University, 2009 [http://theory.cs.princeton.edu/complexity/]
2 Definicję systemów iteracyjnych podał Z. Pawlak w książce „Maszyny matematyczne”, Warszawa 1970, s. 9. Współczesne ich omówienie (jednak bez ścisłych definicji) można znaleźć w opracowaniu: http://www.math.uni.opole.pl/~ebryniarski/sys_iter.pdf. Ścisłą definicję można znaleźć w Andrzej Blikle, „Matematyka a informatyka — konflikty i związki” [w: Informatyka, IX/1972, http://delibra.bg.polsl.pl/Content/3209/Nr%209_72.pdf]. Później Z. Pawlak stworzył bardziej złożony model maszyny programowanej [„A mathematical model of digital computers” ] (http://bcpw.bg.pw.edu.pl/dlibra/docmetadata?id=1709&from=publication)
3 http://osilek.mimuw.edu.pl/index.php?title=Z%C5%82o%C5%BCono%C5%9B%C4%87_obliczeniowa/Wyk%C5%82ad_2:_Inne_modele_dla_z%C5%82o%C5%BCono%C5%9Bci
4 Ściśle rzecz ujmując, funkcja przejścia wciąż będzie mieć taką samą złożoność jak pamięć (bo wszystkie komórki pamięci muszą w niej być jakoś połączone bramkami).